Égi koordináták részleteiről…
Bevezetés
A jelen írásomban kizárólag ismeretterjesztő céllal és módon szeretném áttekinteni azt, hogy
egy adott csillag elméleti koordinátáit a gyakorlatban hogyan értelmezzük. Szeretném
kihangsúlyozni, hogy az elmélkedés nem felel meg maradéktalanul sem a tudományos, sem a
filozófiai szabályoknak: ehhez sem képzettségem, sem felkészültségem nincsen.
Természetesen igyekszem a magyar gyakorlatban használt szakszavakat, fogalmakat
alkalmazni, de ez nem biztos, hogy maradéktalanul sikerül.
Olvasóimnak a megértéshez alapszinten ismernie kell a koordinátarendszereket és a
koordinátákat befolyásoló fizikai jelenségeket, ugyanis csak az utóbbiak hatását boncolgatom.
Ugyanakkor nincs szükség semmilyen komolyabb matematikai ismeretre: az írásban egyetlen
képlet sem található. Így a téma mélyebb ismereteire vágyóknak forrásként a Marik Miklós
szerkesztésében megjelent Csillagászat c. könyvet tudom melegen ajánlani.
Az Univerzum
Az emberiség tudásának gyarapodásával környezetének egyre nagyobb részét ismerte meg, és
ennek a folyamatnak ma sem látjuk a végét. Kezdetben a Föld, a körülötte keringő
bolygócsillagok, és az egészet határoló állócsillagok szférája volt a világ. A megfigyelésen
alapuló csillagászat mintegy ötszáz évvel ezelőtt rendezte át a belső szerkezetet (Kopernikusz
heliocentrikus rendszere), míg a Naprendszerből kitekintéshez a távcső segítségével többek
között William Herschel fogott hozzá a Tejútrendszer feltérképezésével. Hogy egyes észlelt
objektumok a Galaxison is túl, nagyságrendekkel távolabb vannak, annak megfigyelésekkel
történő felderítése csupán a 20. sz. elején kezdődött, Harlow Shapley, Edwin Hubble és a kor
egyre nagyobb teleszkópjainak köszönhetően. Ma 14 milliárd fényév távolságig látunk el:
eddig tart térben és időben az ismert Világegyetem, az Univerzum.
Azonban eszmefuttatásom sokkal kisebb távolságokig terjed, tekintettel arra, hogy írásom a
pontszerű objektumok, azaz a csillagok koordinátáival foglalkozik. A Tejútrendszer átmérője
kb. 150 ezer fényév, a szabad szemmel látható csillagok távolsága pedig nem több 3-4 ezer
fényévnél. De a csillag távolsága is csak annyiban érdekel bennünket, amennyiben
befolyásolja iránykoordinátájának számértékét.
Távolságok
A csillagászatban a távolságok mérésére több mértékegység van használatban; növekvő
sorrendben: kilométer, Cs.E. (csillagászati egység, a Föld és a Nap közepes távolsága), fényév
(az a távolság, amelyet a fény légüres térben egy év alatt befut) és parszek (az a távolság,
ahonnan a földpálya fél nagytengelye 1" szög alatt látszik). Az egységek egymáshoz
viszonyított (általában kerekített) értékeit az alábbi táblázat mutatja:
|
km |
Cs.E. |
fényév |
parszek |
|---|
| km |
1 | 6,7·10-9 | 1·10-13 | 3·10-14 |
|---|
| Cs.E. |
1,49597870·108 | 1 | 1,6·10-5 | 5·10-6 |
|---|
| fényév |
9,46·1012 | 63200 | 1 | 0,3 |
|---|
| parszek |
3·1013 | 206265 | 3,26 | 1 |
|---|
Koordinátarendszerek
A csillagászatban többféle koordinátarendszert használnak, melyeknek itt még a felsorolásától
is eltekintek. Abban viszont megegyeznek, hogy olyan gömbi (szférikus)
koordinátarendszerek, melyeknél a két szögkoordinátán túl a harmadik, a távolság 1. Ez az
egyszerűsítés azért engedhető meg, mert a csillagok a megfigyelés szempontjából tőlünk
végtelen messze, és egymástól is nagy távolságban vannak, így egy képzeletbeli
gömbfelületen, az ún. éggömbön lévőnek tekinthetjük őket. A földrajzi hely megadásához
hasonlóan két szögkoordináta egyértelműen meghatározza az égitestek helyzetét. A
továbbiakban kizárólag a csillagatlaszokban, -katalógusokban alkalmazott egyenlítői
(ekvatoriális) koordinátákról lesz szó. Ennek a szférikus rendszernek az alapsíkja a Föld
egyenlítői síkjának kiterjesztése, az alapirány a tavaszpont iránya, sarkpontjai a Föld
forgástengelyével párhuzamos világtengely által kijelölt égi pólusok; origója a tér tetszőleges
pontján lehet, de általában a Föld középpontja. Két koordinátája a rektaszcenzió és a
deklináció.
Katalógusok, csillagpozíciók
Írásom bizonyos szempontból ellentmondásos témával foglalkozik: azt mondhatjuk, hogy
ahány csillagkatalógus, annyi koordináta! Érdemes-e akkor olyan hatásokkal foglalkozni,
amelyek a pozíciókat esetenként csupán az ívmásodperc tört részével befolyásolják? A válasz
természetesen igen, mert a két dolog elkülönül egymástól. A csillagok valódi pozíciójának
meghatározása az újabb mérési eszközöknek és módszereknek köszönhetően egyre nagyobb
pontosságú, ám ez nem zárja ki a korábbi katalógusok használatát. Másrészt a koordinátákat
módosító fizikai tényezők hatása többé-kevésbé nagy pontossággal meghatározható elméleti
kérdés, aminek számításba vétele a valódi pozíció meghatározásához elengedhetetlen.
Néhány példával szeretném bemutatni a csillagpozíciók fejlődését.
Egy csillag pontos pozíciójának meghatározása nehéz feladat, ezért érthető, hogy a
Fundamentális katalógusok (FK4 és FK5) mindössze 1535 csillag koordinátáit tartalmazzák
0,01" pontossággal. A 320 ezernél több objektumot tartalmazó "Position and Proper Motion"
(PPM) katalógus az egyszerűbb asztrometriai igényeket elégítheti ki, míg a USNO
asztrografikus katalógusa (AC 2000) 140 forrás felhasználásával 4,6 millió csillag redukált
adatait tartalmazza. Alapvetően más alapokon áll a Hipparcos asztrometriai űrprogram: az
azonos nevű katalógus a legfényesebb 120 ezer csillag pozícióját és egyéb adatait tartalmazza
minden eddiginél nagyobb pontossággal; a vele egyidőben végrehajtott Tycho program 2,5
millió csillagról szolgáltatott valamivel pontatlanabb mérési eredményeket.
Egy csillag koordinátái
Tételezzük fel, hogy egy csillag helyzetét tetszőleges pontossággal ismerjük. Magától
értetődik, hogy a pozíciót megadó koordináták állandóak, ha a koordinátarendszer és az
égitest nyugalomban van. A valóság természetesen más:
- egy kívülálló számára bizonyára meglepő, hogy az ember által - részben önkényesen -
megválasztott koordinátarendszer változik a legnagyobb mértékben (ennek külön
tárgyalt esete a parallaxis);
- a csillag mozog a térben: ennek a látóirányra merőleges komponenseit sajátmozgásnak
nevezzük.
Külön csoportként említhetők azok a fizikai jelenségek, tényezők, amelyek egy égi pozíció
megállapítása során a koordinátákat a valóstól eltérőnek mutatják:
- a légkör hatásáról annyit külön érdemes megjegyezni, hogy a csillagpozíció pontos
meghatározásának legnagyobb gátja;
- végül - mivel a megfigyelő a Földdel együtt bizonyos sebességgel mozog - az
aberrációnak nevezett jelenség is megváltoztatja a tényleges irányt.
A továbbiakban egyenként áttekintjük a koordinátákat befolyásoló tényezőket - az egyes
jelenségek magyarázatát meghagyva a szakkönyveknek -, de előtte még a távolság látószög-vonatkozásait.
(Mivel itt a jelenség bemutatása a lényeg, ezért a számértékek általában
kerekítettek, illetve a nagy és kis számok célszerűen normál alakban vannak írva.)
A parszek definíciójából következik, hogy 100 pc távolságból nézve egy Cs.E. távolság
1/100" szög alatt látszik. A Föld sugarának látószöge ennek 150·106/6·103-od része,
azaz 4·10-7", 1 km pedig 7·10-11": ha koordinátarendszerünk
kezdőpontja 1 km-rel elmozdul, akkor a
csillagpozíció ívmásodperc értékében maximum a tizedik számjegynél lesz eltérés (attól
függően, hogy az elmozdulás iránya a csillag irányával mekkora szöget zár be).
Az iménti távolságok példának választása nem véletlen: a csillag helyzetének
megállapításánál a koordinátarendszer kezdőpontja a választott földrajzi hely, és ez a térbeli
hely folyamatosan változik a Föld forgása és Nap körüli keringése következtében,
maximálisan 2 Cs.E. távolsággal.
A fejezet kezdő mondata szerint egy adott koordinátarendszerben ismerjük egy csillag pontos
pozícióját: miként kerülhetnek szóba az ezt módosító tényezők?
Egyrészt több okból is szükségünk lehet ennek az égitestnek egy adott pillanatban, adott
helyen érvényes látszólagos koordinátáira; másrészt ha egy pozíciós asztrometriával
foglalkozó csillagász meg akarja határozni egy csillag abszolút koordinátáit, akkor ezt az
általa mért látszólagos koordináták redukciójával - a fentebb felsorolt jelenségek figyelembe
vételével - teheti meg. Ám írásom mégsem erre a két esetre gondolva készült! Ha egy
számítógépes csillagászati programban egy csillagra vonatkozóan több - egymástól
kisebb-nagyobb mértékben eltérő - koordinátát is találunk, akkor egy kevésbé képzett amatőrnek
gondot okozhat az értelmezés: ezt szeretném a magam egyszerű módján segíteni.
A
magyarázatot az Astronomical Almanac v5.4 program példáinak segítségével illusztrálom. A
vizsgálódás szempontjából nincs jelentősége, hogy egyes példaidőpontok nappalra esnek vagy
sem, sőt esetenként az is lényegtelen, hogy a csillag a horizont alatt van-e. Annak, hogy a
példák zömében 1986. jan. 1-jei dátum szerepel, az az egyszerű magyarázata, hogy a
programnak ez az alapértelmezett dátuma. A szemléltető ábráknál a koordinátatengelyek
iránya és a módosító hatások előjele az egyenlítői rendszernek megfelelő, azaz a vízszintes
tengelyen van feltüntetve a rektaszcenzió balra növekvően, a függőleges tengelyen pedig
a deklináció. Az éggömbrészletet reprezentáló ábrák háttérszíne fekete.
Légköri fénytörés (refrakció)
Csillagok esetén egy adott pillanatban a legnagyobb irányeltérést Földünk légköre okozhatja.
Az eltérés az objektum horizont fölötti magasságától függ: zenitben 0, a horizonton pedig 30'-
nél kicsivel nagyobb. Ennek a hatásnak leggyakrabban említett példája, hogy a Nap vagy a
Hold (átmérőjük kb. 30') még a horizont alatt van, amikor a refrakció következtében már
teljes terjedelmében látható, ugyanis a légkör mindig emeli az égi objektumokat. A fénytörés
magasság szerint nem lineáris hatású, 45 fokos magasságnál 1' körüli érték. Elvileg is függ a
levegő hőmérsékletétől és nyomásától, de még a beeső fény hullámhosszától is, ezért
kiszámítása meglehetősen bonyolult matematikai függvényekkel történik. Az ekvatoriális
koordinátákra vonatkozóan a déli és északi irányban, azaz a meridiánban tartózkodó
csillagoknál a refrakció csak a deklinációt növeli, kelet és nyugat felé a rektaszcenziót érintő
komponens fokozatosan növekszik az előbbi rovására - természetesen elsősorban
magyarországi észlelőhelyre gondolva.
Példaként nézzük meg az Aldebaran refrakció okozta koordináta-változását (Hely és idő: Vaskút, 1986.01.01.):
-15h 00m 00.000s UT (kelés után másfél órával), 0 oC, 1010 mbar:
atmospheric refraction 0.056 deg dRA -10.016s dDec 139.97"
Altitude 16.074 deg, Azimuth 82.682 deg
-20h 38m 20.000s UT (delelés táján), légköri paraméterek mint előbb:
atmospheric refraction 0.009 deg dRA 0.055s dDec 32.80"
Altitude 60.374 deg, Azimuth 181.912 deg
A légköri refrakciónak a horizontális rendszerben mért magasságkoordinátára gyakorolt hatását
grafikusan láthatjuk az alábbi ábrán:
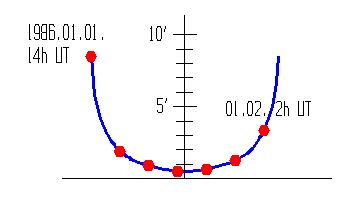 Az Aldebaran 1986. január 1-jén Vaskúton 13:18 UT-kor kel, 20:34 UT-kor delel, és január 2-án 3:46
UT-kor nyugszik. A görbét felosztó piros színű jelek 2 óránként követik egymást. A vízszintes
koordinátatengelyen az idő, a függőleges tengelyen a refrakció szögértéke szerepel ívpercben.
Az Aldebaran 1986. január 1-jén Vaskúton 13:18 UT-kor kel, 20:34 UT-kor delel, és január 2-án 3:46
UT-kor nyugszik. A görbét felosztó piros színű jelek 2 óránként követik egymást. A vízszintes
koordinátatengelyen az idő, a függőleges tengelyen a refrakció szögértéke szerepel ívpercben.
A teljesség (és érdekesség) kedvéért bemutatom a refrakció okozta egyenlítői koordináták változását is:
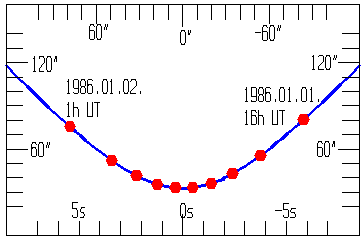 Az ábra lényegében a delelés környéki ±4,5 óra alatt kialakuló koordinátaváltozást tudja bemutatni,
mert a keléshez, nyugváshoz közelebbi időben az eltérés az itt láthatónak a húszszorosát is eléri. A
refrakciós változás rektaszcenzió és deklináció szerinti komponenseinek aránya az észlelés földrajzi
szélességétől függ. A piros korongok a kerek órákat jelzik.
Az ábra lényegében a delelés környéki ±4,5 óra alatt kialakuló koordinátaváltozást tudja bemutatni,
mert a keléshez, nyugváshoz közelebbi időben az eltérés az itt láthatónak a húszszorosát is eléri. A
refrakciós változás rektaszcenzió és deklináció szerinti komponenseinek aránya az észlelés földrajzi
szélességétől függ. A piros korongok a kerek órákat jelzik.
Minél sűrűbb a levegő (kisebb hőmérséklet, nagyobb légnyomás), annál nagyobb a refrakció mértéke:
- UT 0, 12 oC, 1010 mbar: atmospheric refraction 0.020 deg dRA 3.424s dDec 52.07"
Altitude 38.838 deg, Azimuth 251.880 deg
- UT 0, 0 oC, 1010 mbar: atmospheric refraction 0.021 deg dRA 3.575s dDec 54.36"
Altitude 38.839 deg, Azimuth 251.880 deg
- UT 0, 0 oC, 1020 mbar: atmospheric refraction 0.021 deg dRA 3.610s dDec 54.90"
Altitude 38.839 deg, Azimuth 251.880 deg
Aberrációk
A megfigyelő sebessége a Föld forgásából és a Nap körüli keringéséből adódik: az előbbinek
a csillagról érkező fény irányára gyakorolt hatását napi, az utóbbiét évi aberrációnak
nevezzük. Amennyiben pontosan a csillag felé irányul a mozgás, akkor az aberráció értéke 0,
ha a csillag iránya és a mozgás iránya 90o-os szöget zár be, akkor az aberráció értéke
maximális.
A napi aberrációt okozó kerületi sebesség függ a megfigyelési pont forgástengelytől mért
távolságától, azaz a földrajzi szélességtől, így maximális az egyenlítőn, és 0 a Föld pólusain.
Ha a sebesség a legnagyobb, valamint a vizsgált csillag és a mozgás iránya által bezárt szög
90o, akkor az aberráció 0,319", amit a napi aberráció állandójának nevezünk. Az égi egyenlítő
környéki csillagoknak túlnyomóan a rektaszcenziója módosul, és mivel a Föld forgásából
adódó sebességvektor keleti irányú, ezért a meridián környékén a legnagyobb a napi
aberráció.
A Föld pálya menti sebessége az ismert Kepler-törvények szerint kis mértékben változik. Ha
első közelítésben ettől eltekintünk, vagyis a pályát körnek vesszük, akkor a napi aberrációhoz
hasonlóan az évi aberráció maximális lehetséges értéke és egyúttal az állandója 20,49552".
Ennek eredményeként az ekliptika pólusa, mint egy szférikus pont kerekítve 20,5" sugarú
kört, az ekliptika síkjában lévő csillag 41" hosszúságú egyenes szakaszt ír le egy év alatt; a
köztes pontok ebből következően 41" nagytengelyű ellipsziseket rajzolnak ki az éggömbön.
Példaként nézzük meg a Shedir (alfa Cas) koordinátáinak aberrációs változását (Hely és idő: Vaskút,
1986.01.01.):
- 17:00 UT (felső delelés után):
annual aberration dRA -0.007s dDec 16.44"
diurnal aberration dRA 0.027s dDec 0.02"
- 22:00 UT:
annual aberration dRA -0.016s dDec 16.42"
diurnal aberration dRA 0.004s dDec 0.18"
Itt hívom fel a figyelmet arra, hogy az égi pólusok közelében lévő égitesteknél kicsi ívmásodpercben
kifejezett szögtávolság jóval nagyobb rektaszcenzió számérték változást eredményez. Ennek
bemutatására álljanak itt a Sarkcsillagra (Polaris) vonatkozó adatok (Hely és idő: Vaskút,
1986.01.01.):
Astrometric J2000.0: R.A. 2h 31m 45.892s Dec. 89d 15' 50.94"
Astrometric B1950.0: R.A. 1h 48m 54.056s Dec. 89d 01' 43.20"
Astrometric of date: R.A. 2h 17m 19.093s Dec. 89d 12' 04.22"
annual aberration dRA 51.135s dDec 18.19"
nutation dRA -38.213s dDec 0.90"
Az alábbi ábrák az Aldebaran évi és napi aberrációját mutatják:
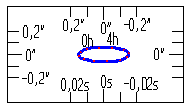 A napi aberráció az Aldebaran esetében, Vaskútra vonatkoztatva nagyon kicsi, az évi aberráció század
része: a fél nagytengely mintegy 0,2". Ahhoz, hogy az ábra valamennyire is értékelhető legyen, az évi
aberráció ábrájához viszonyítva 16-szorosára kellett nagyítani. A piros jelek ebben az esetben két órás
időközöket jelölnek. (1986. jan. 1.)
A napi aberráció az Aldebaran esetében, Vaskútra vonatkoztatva nagyon kicsi, az évi aberráció század
része: a fél nagytengely mintegy 0,2". Ahhoz, hogy az ábra valamennyire is értékelhető legyen, az évi
aberráció ábrájához viszonyítva 16-szorosára kellett nagyítani. A piros jelek ebben az esetben két órás
időközöket jelölnek. (1986. jan. 1.)
Az eddig bemutatott két hatás az észlelt csillagot a valódi irányától eltérő helyen mutatja. Ha
a távcső osztott körein leolvasott koordinátákat a refrakció és a napi aberráció pillanatnyi
értékével korrigáljuk, akkor megkapjuk a csillag földrajzi helytől független, ún. látszó
koordinátáit, illetve látszó helyét, míg ha az évi aberrációt is számításba vesszük, akkor a
valódi (asztrometrikus) koordinátához jutunk, amely a mérés időpontjára nézve érvényes
pozíció. Más időpontra ugyanezen égitest valódi helye ettől eltér, ami a továbbiakban kerül
ismertetésre.
A koordinátarendszer helyzete
Bevezetőként rögzítsük le, hogy egy csillagászati szférikus koordinátarendszer helyzetének
vizsgálatát két részre bonthatjuk:
- a kezdőpont (origó) térbeli helye
- a koordinátarendszer térbeli állása.
Koordinátarendszerünk kezdőpontját tekintve lehet:
- topocentrikus (a tér meghatározott pontjában, de esetünkben mindenképpen a Föld felszínén)
- geocentrikus (a Föld középpontjában)
- heliocentrikus vagy baricentrikus (a Nap vagy a Naprendszer középpontjában).
Az első két esetnél a kezdőpont folyamatosan mozog a térnek egy meghatározott
tartományában, miközben a koordinátarendszert önmagával párhuzamosnak tekintjük. A
harmadik esetnél az origót nyugvónak tekinthetjük. A kezdőpont helyéből adódó
koordináta változásokkal a parallaxist tárgyaló részben ismerkedünk meg.
Precesszió és nutáció
Korábban már említésre került, hogy az ekvatoriális koordinátarendszer definiálása a Földhöz
kapcsolódik, és ebből kifolyólag térbeli helyzete nem állandó: alapsíkja, polártengelye és az
alapirány a Naprendszer tagjainak egymásra gyakorolt gravitációs hatása következtében megváltozik
(elfordul, elbillen). A változást előidéző fizikai jelensége(ke)t luniszoláris és planetáris precessziónak,
valamint nutációnak nevezzük. Arról van szó tehát, hogy vonatkoztatási rendszerünk helyzete
pillanatról pillanatra módosul, ha nem is nagyon nagy mértékben, de annál bonyolultabban.
Ennek kezelése a gyakorlatban úgy történik, hogy az ekvatoriális koordinátákat bizonyos
kerek időpontokban fennálló helyzetre vonatkozóan adjuk meg, a koordináták mellett
feltüntetve ezt az időpontot is, amit epochának nevezünk. Régebben a javasolt
epochák a 25-tel osztható évszámok voltak (bár van ettől eltérő is, pl. a Bonner
Durchmusterung 1855-ös epochája); az 1950-es epochájú koordináták után 10-20 éve
leginkább a J2000-es ekvinokcium használatos. Bocsánatos elfogultsággal megemlíteném a
Meteor csillagászati évkönyvet, amely - mint az évkönyvek általában - a Magyarországról
látható fényesebb csillagoknak az adott év közepére vonatkozó egyenlítői koordinátáit közli.
A precesszió következtében a rektaszcenzió - a pólusok szűk környezetének kivételével - az
időben előre haladva mindig növekszik, míg a deklináció a rektaszcenziótól függően nő vagy
csökken. Mivel a néhány tíz év alatt nagyjából lineáris precessziós változáshoz a nutáció 9"
amplitúdójú hullámként adódik hozzá, ezért ettől adott esetben eltekinthetünk: az alábbi példa
is mutatja, hogy a nutáció ívmásodperc nagyságrendben módosítja az égitest pozícióját, ami a
14 év alatti precesszió okozta változásnál nagyságrenddel kisebb. A nutáció számszerű
értékének egy grafikus ábrázolását tekinthetjük meg a Grafikus összefoglalás c. alfejezetben.
A katalógusból vagy térképről származó ekvatoriális koordinátákból az adott időpontra
érvényes közelítő koordinátákat - a számítástechnikai korszak előtt - általában precessziós
táblázatok segítségével határoztuk meg.
Nézzük meg az alfa Andromedae (Alpheratz) példáján a koordinátarendszer
elfordulásából adódó változásokat:
Astrometric J2000.0: R.A. 0h 08m 23.265s Dec. 29d 05' 25.58"
Astrometric B1950.0: R.A. 0h 05m 48.404s Dec. 28d 48' 43.86"
- Astrometric of date 1986.01.01. 0 UT: R.A. 0h 07m 39.856s Dec. 29d 00' 45.16"
nutation dRA -0.828s dDec -3.45"
- Astrometric of date 1986.01.08. 0 UT: R.A. 0h 07m 39.915s Dec. 29d 00' 45.54"
nutation dRA -0.820s dDec -3.41" (egy hét alatt a különbség minimális)
- Astrometric of date 1995.01.01. 0 UT: R.A. 0h 08m 07.755s Dec. 29d 03' 45.42"
nutation dRA 1.031s dDec 4.58" (a nutáció ellentétesre fordul 9 év - fél nutációs periódus - alatt)
Parallaxis eltérés
Az aberrációhoz hasonlóan a koordinátarendszer kezdőpontjának változása is kétféle: a Föld
forgásából adódóan napi, a keringéséből adódóan évi parallaxisról beszélünk. A fejezet
bevezetőjében említettek szerint a Föld átellenes pontjaiból nézve, merőleges rálátás esetén
egy 10 pc távolságban lévő csillag egy százezred ívmásodpercnél kisebb irányeltérést
szenved. Ebből kifolyólag a napi parallaxist gyakorlatilag csak a naprendszerbeli égitestek
esetén szokás számításba venni.
Az évi parallaxis szintén meglehetősen kis szögérték a Naprendszeren kívüli égitestek
esetében. Mivel a legközelebbi csillag is 1 parszeknél nagyobb távolságban van, ezért az évi
parallaxis a heliocentrikus pozíciótól mindenképpen ±1"-nél kisebb eltérést okoz, de legtöbb
esetben nagyságrend(ekk)el kisebbet.
Példaként a legközelebbi csillag, az alfa Centauri parallaktikus koordináta-változását mutatom be:
1986.01.01. 0 UT Astrometric J2000.0: R.A. 14h 39m 42.941s Dec. - 60d 50' 17.07"
A továbbiak sajátmozgás nélkül:
- 1986.01.01. 0 UT Astrometric J2000.0: R.A. 14h 39m 35.967s Dec. - 60d 50' 07.30"
- 1986.04.01. 0 UT Astrometric J2000.0: R.A. 14h 39m 35.936s Dec. - 60d 50' 07.98"
- 1986.07.01. 0 UT Astrometric J2000.0: R.A. 14h 39m 35.802s Dec. - 60d 50' 07.60"
- 1986.10.01. 0 UT Astrometric J2000.0: R.A. 14h 39m 35.829s Dec. - 60d 50' 06.91"
Ugyanez látható a következő ábrán:
A csillagok sajátmozgása
A csillagok sajátmozgását nagyobb időköz és pontosabb koordináták szükségessége esetén
számításba kell venni, bár az esetek többségében jóval kisebb - vagy ha nem ismert, akkor
nullának tekintendő - mint az évente 10"-et is meghaladó Barnard-csillag sajátmozgása. A
katalógusokban általában a rektaszcenzió- és deklinációirányú sebességkomponensek vannak
megadva a megfelelő mértékegységben; ekkor a számítás elemi matematikai műveletekkel elvégezhető.
A sajátmozgás okozta koordinátaváltozás illusztrálásához nem szükséges
számítógépes programot igénybe
venni. Az alfa Cen évi sajátmozgása 0,075 s ill. -0,5", ezért pl. 20 év alatt rektaszcenziója 1,5 (20*0,075)
időmásodperccel növekszik, deklinációja 10 (20*(-0,5)) ívmásodperccel csökken.
Numerikus összefoglalás
Először is eredeti formában bemutatom az Astronomical Almanach v5.4 számítógép program
(DOS) bemenő adatait, valamint a számítás eredményét az Aldebaran csillagra vonatkozóan.
Steve Moshier's Ephemeris Program v5.4
Planetary and lunar positions approximate DE404.
Terrestrial east longitude 18.9860 deg
geocentric latitude 45.9157 deg
Earth radius 0.99828
temperature 12.0 C
pressure 1010 mb
Input time is UT.
Enter starting date of tabulation
Calendar date: Year (1986) ?
Month (1-12) (1) ?
Day.fraction (1.000000) ?
Time: Hours (0) ?
Minutes (0) ?
Seconds (0.000000) ?
1986 January 1 Wednesday 0h 00m 54.870s TDT
1986 January 1 Wednesday 0h 00m 00.000s UT
2000 04 35 55.237 16 30 33.39 0.439 -18.97 54.0 0.0480 0.85 Aldebaran
alpha Tauri (Aldebaran
JD 2446431.50, 1986 January 1 Wednesday 0h 00m 54.870s TDT
1986 January 1 Wednesday 0h 00m 00.000s UT
Astrometric J2000.0: R.A. 4h 35m 55.174s Dec. 16d 30' 36.04"
Astrometric B1950.0: R.A. 4h 33m 03.076s Dec. 16d 24' 30.72"
Astrometric of date: R.A. 4h 35m 06.961s Dec. 16d 28' 54.93"
elongation from sun 148.88 degrees, light defl. dRA 0.000s dDec 0.00"
annual aberration dRA 1.243s dDec 1.56"
nutation dRA -0.684s dDec 5.15"
Apparent: R.A. 4h 35m 07.520s Dec. 16d 29' 01.68"
Local apparent sidereal time 7h 57m 20.753s
approx local meridian transit 20h 38m 19.897s UT (date + -0.14005)
rises approx 13h 24m 16.461s UT, sets approx 3h 52m 23.332s UT
diurnal aberration dRA 0.010s dDec 0.05"
atmospheric refraction 0.020 deg dRA 3.424s dDec 52.07"
Topocentric: Altitude 38.838 deg, Azimuth 251.880 deg
Topocentric: R.A. 4h 35m 10.954s Dec. 16d 29' 53.80"
- Az angol neveket nem "magyarosítom" azért, hogy angol nyelvű programokban az
egyeztetés egyértelmű legyen.
- A program több olyan (rész)eredményt is kiír, amelyről írásomban nem tettem
említést, részben azért, mert nem tartozik szorosan a tárgyhoz.
- A program bemenő adatként kijelzi a
csillag kiinduló adatait, ami egy fájlban
található: egyes adatok jelentését nem látom szükségesnek itt ismertetni.
- Az "Astrometric" koordináták tartalmazzák a csillag sajátmozgását és a parallaxist; az
adott epochával megkülönböztetett koordinátarendszerek a precessziós elmozdulásnak felelnek meg.
A valós koordinátákról szólva fontos tudatosítanunk azt, hogy ezek a koordinátarendszer adott
időpontbeli helyzetének (epocha), de a választott időnek megfelelő égi pozícióra
vonatkoznak, ami az esetek többségében nem azonos időpontot jelent. A nyomtatott
csillagkatalógusok és -atlaszok esetében technikai okból nem áll rendelkezésünkre más-más időpontban
érvényes koordináta, de a számítógépes programok ezt már számítják és kijelzik. Ennek azért
van jelentősége, mert egy tetszőleges égitest valós koordinátái a mérés idejére nézve igazak és
más epochára vonatkozóan nagy pontossággal számíthatók, azonban más időpontban - még
ha ismerjük is az objektum távolságát és sajátmozgását, ezen adatok pontatlansága miatt -
egyre nagyobb hibával terheltek. Ezt a Guide planetárium program a Hipparcos katalógusban
szereplő csillagok esetében, a részletes adatkijelzés során, szemléletesen mutatja:
RA (J2000.0): 04 35 55.20
declination +16 30 35.1
(Above is the computed position for J1991.25)
Eszerint a Hipparcos katalógus a program során ténylegesen mért
koordinátákat az 1991,25 időpontra "átlagolva", de
a J2000 epochájú koordinátarendszernek megfelelően tartalmazza - a pozíció számított hibaértékével
együtt, ami itt nem kerül kijelzésre.
1991,25-kor:
J2000 position at current date (proper motion included):
Right ascension: 4h35m55.2005s
Declination: N16 30' 35.142"
(Above is ±0.8 milliarcseconds in RA, ±0.5 milliarcseconds in dec
1986.01.01-kor:
J2000 position at current date (proper motion included):
Right ascension: 4h35m55.1776s
Declination: N16 30' 36.136"
(Above is ±4.5 milliarcseconds in RA, ±3.3 milliarcseconds in dec)
Láthatjuk, hogy az eredeti ±0,8 mas ill. ±0,5 mas pontosság
5,25 év különbséggel már csak ±4,5 mas ill. ±3,3 mas.
A Guide által használt legpontosabb földi csillagkatalógus, a PPM képernyőn megjelenített Aldebaran
adatai jobban lefedik a tárgyalt koordinátaváltozatokat.
A "current epoch" 1986.01.01:
Comments from the PPM catalog:
PPM 120061
Magnitude: 0.8
J2000 RA: 04h 35m 55.237s
J2000 dec: +16 30' 33.39"
Proper motion in RA: 0.0044 RA seconds/year
Proper motion in dec: -0.190 arcseconds/year
J2000 position at epoch:
Right ascension: 4h35m55.175s
Declination: N16 30' 36.05"
Mean position at current epoch:
Right ascension: 4h35m06.960s
Declination: N16 28' 54.93"
Apparent position at current epoch:
Right ascension: 4h35m07.518s
Declination: N16 29' 01.67"
(Above is ±17.1 milliarcseconds in RA, ±21.4 milliarcseconds in dec
Vegyük sorra a megadott koordinátákat!
-
J2000 RA és J2000 dec:
az Aldebaran 2000-es ekvatoriális koordinátarendszerben, 2000.0
időpontban létező valós koordinátái, az FK5 katalógussal egyezően.
Vessük össze a Guide által a Hipparcos adatokból számítottakkal:
J2000 position at current date [2000.01.01.]
(proper motion and parallax included):
Right ascension: 4h35m55.2370s
Declination: N16 30' 33.478"(Above is ±7.5 milliarcseconds in RA, ±5.5 milliarcseconds in dec)
A rektaszcenzió egyezik, a deklinációnál fennálló 88 mas különbség jelentősen eltér a
Hipparcos ±5,5 mas hibahatárától.
-
J2000 position at epoch:
az Aldebaran 2000-es ekvatoriális koordinátarendszerben, 1986.01.01. időpontban létező valós koordinátái.
-
Mean position at current epoch:
az Aldebaran 1986.01.01. epochájú ekvatoriális koordinátarendszerben, 1986.01.01. időpontban létező valós koordinátái.
-
Apparent position at current epoch:
az Aldebaran 1986.01.01. epochájú ekvatoriális koordinátarendszerben, 1986.01.01. időpontban létező látszó koordinátái, amelyek
tartalmazzák a nutációt és az évi aberrációt is.
Grafikus összefoglalás
A jelenségek megértéséhez, bemutatásához hatásos eszköz a grafikus módszer; gondolom az
olvasók közül sokan egyetértenek ezzel. Természetesen a grafikonoknak hátránya is van,
mégpedig az, hogy az alkalmazható méretarány sok esetben nem teszi lehetővé a pici
különbségek érzékeltetését. Így van ez már az első esetben is, a koordináták precesszió,
sajátmozgás és évi parallaxis miatti változásának vizsgálatánál.
Ebben az alfejezetben - a numerikus összegzéssel egyezően - szintén az Aldebaran a
példacsillag, a vizsgált időszak az 1986. év.
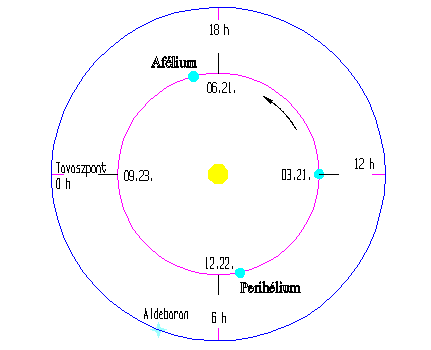 A bal oldali ábra a Föld nevezetes pozícióit
mutatja az éves keringés során. A külső kör az éggömböt jelképezi a megfelelő rektaszcenzió
értékekkel, valamint az Aldebaran irányával.
A bal oldali ábra a Föld nevezetes pozícióit
mutatja az éves keringés során. A külső kör az éggömböt jelképezi a megfelelő rektaszcenzió
értékekkel, valamint az Aldebaran irányával.
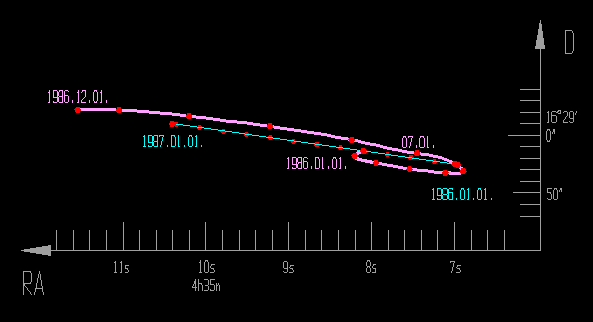
Az ábrán nem érzékeltethető az Aldebaran +0,0044 s/év ill. -0,190 "/év mértékű sajátmozgása,
valamint a precessziós változás is lineárisnak vehető (a kék színű szakaszon található piros
pontok 30 naponként követik egymást). A rózsaszínű görbe a precesszió és az évi aberráció
együttes hatására létrejövő pozíciókat mutatja 1985.12.01-től 1986.12.01-ig, az egyes
hónapok első napjának UT 0 óráját piros színű koronggal jelölve. (Minden ábrára vonatkozik,
hogy a görbék egyes helyeken látható "törése", szabálytalan íve a felhasznált pozíciók
kerekített voltából adódik.)
Egy év leforgása alatt az egyenlítői koordinátákat legnagyobb mértékben a precesszió
módosítja, de láthatóan az évi aberráció sem sokkal kevesebb. Ha összevetjük a görbét az évi
aberrációt bemutató ábrával, akkor megállapítható, hogy az aberráció hatására márciusig a
rektaszcenzió nagyobb, ezt követően szeptember elejéig kisebb, majd ismét nagyobb, mint
amennyi egyedül a precesszióból adódóan lenne. A méretarányos ábrán jól látszik, hogy az
évi aberráció a deklinációt jóval kisebb mértékben befolyásolja, valamint az is, hogy a
"pálya" nagyon hasonlít a bolygók által az égbolton egy év alatt leírt hurkokhoz.
Természetesen ne felejtkezzünk el arról, hogy a jelen esetben a koordinátarendszer elbillenése
és a Földdel együtt keringő megfigyelő sebessége okozza a koordináták változását!
A nutáció - melynek egy hónapon belül is
viszonylag jelentős a változása - bemutatásához az
1986. április 21.-május 17. közti időszakot választottam, egyrészt a használható méretarány
érdekében, másrészt mert itt van a látszó koordináta görbéjének inflexiós pontja. Először az
egyes tényezők hatását tekintsük meg egy "nagyobb léptékű" éggömbrészleten.
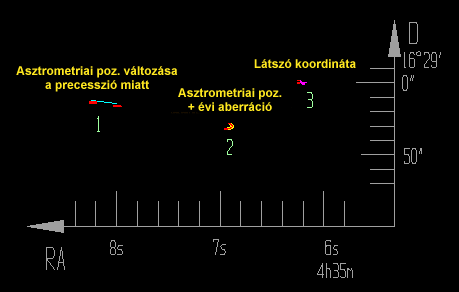
Az 1 jelzésű helyen van az Aldebaran a valóságban:
a precessziós koordinátaváltozás még
ebben a méretarányban is szépen látható (kék szakasz); a precessziós változás lineáris, ezért
azt külön kinagyítva szükségtelen lenne ábrázolni. A 2 helyen látszik a csillag az évi aberráció
következtében, és a 3 helyen a nutációt is figyelembe véve.
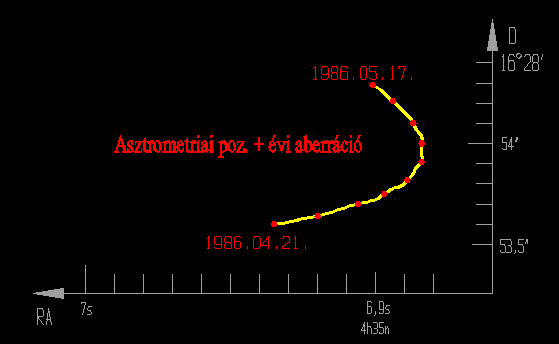
Az Aldebaran koordinátái az évi aberráció hatására. A piros körök minden harmadik napot
jelölik. A görbe azért hullámos, mert a napokra számított pontokra épül.
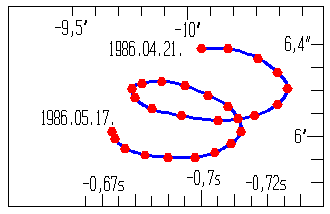 A nutáció számos, az ekvatoriális koordinátarendszert befolyásoló tényezőt foglal magába, de
közülük legjelentősebb Holdunk gravitációs hatása. Az ábrából látható, hogy egy hónap alatt
egy dupla spirál rajzolódik ki, amelynek "amplitúdója" néhány tized ívmásodperc.
A nutáció számos, az ekvatoriális koordinátarendszert befolyásoló tényezőt foglal magába, de
közülük legjelentősebb Holdunk gravitációs hatása. Az ábrából látható, hogy egy hónap alatt
egy dupla spirál rajzolódik ki, amelynek "amplitúdója" néhány tized ívmásodperc.
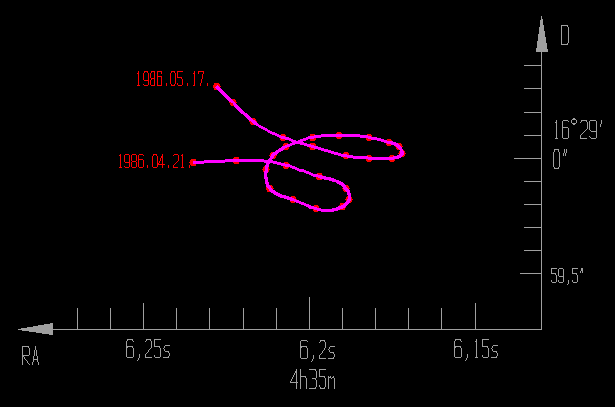
A fenti ábra mutatja a látszó koordináták alakulását a vizsgált időszakban. Nagyon látványos,
hogy a nutáció, amellett, hogy 6 ívmásodperccel "megemeli" és 0,7 időmásodperccel
nyugatra tolja a koordinátákat, parányi dupla hurkot varázsol az évi aberráció ellipszisének a
csúcsára. Vegyük észre, hogy a nutáció ábráján a felső spirál adja a látszó koordináta-görbe
alsó hurkát; az aberráció deklináció növelő komponense emeli az alsó nutációs spirált az alsó
hurok fölé.
Természetesen az itt bemutatott nutációs koordinátaváltozás egész évben létezik, de az évi
aberráció hatása gyengítheti, eliminálhatja. Emiatt a látszó koordináta éves görbéjénél a
nutáció nincs számításba véve, mivel az adott léptéknél és a hónapok első napja pozíciójának
felhasználása folytán zavaró lenne és nem nyújtana értékelhető többlet információt.
Zárszó
Azon ritka kivételek közé tartozom, aki amatőrcsillagász megfigyeléseit kezdettől fogva
osztottkörös beállítással végzi, így magától értetődik, hogy a koordinátarendszerek témájában
közvetlenül érintett voltam és vagyok. Természetesen saját készítésű távcsövemnél és a
megfigyeléseknél az ívmásodperc pontosságú koordinátáknak nincs jelentősége, de például a
precessziós hatást két epocha - az 1950-es és a 2000-es - között félúton már érdemes volt
számításba venni. Ettől függetlenül a mostani vizsgálódásra a Guide számítógépes
programban található, egymástól minimális mértékben különböző koordináták értelmezése
késztetett. Remélem, hogy kíváncsiságommal nem vagyok egyedül, és a fenti - esetleg
kisebb-nagyobb hiányosságokkal is terhelt - eszmefuttatásommal segíthettem néhány
amatőrtársamnak az asztrometria alapjai eme részének megértésében. Építő hozzászólást vagy
kérdést örömmel várok.
Hivatkozások: Astronomical Almanac v5.4 program (DOS)
Guide 7.0 program (Windows)
Vaskút, 2006.03.14.
 Az Aldebaran 1986. január 1-jén Vaskúton 13:18 UT-kor kel, 20:34 UT-kor delel, és január 2-án 3:46
UT-kor nyugszik. A görbét felosztó piros színű jelek 2 óránként követik egymást. A vízszintes
koordinátatengelyen az idő, a függőleges tengelyen a refrakció szögértéke szerepel ívpercben.
Az Aldebaran 1986. január 1-jén Vaskúton 13:18 UT-kor kel, 20:34 UT-kor delel, és január 2-án 3:46
UT-kor nyugszik. A görbét felosztó piros színű jelek 2 óránként követik egymást. A vízszintes
koordinátatengelyen az idő, a függőleges tengelyen a refrakció szögértéke szerepel ívpercben. Az ábra lényegében a delelés környéki ±4,5 óra alatt kialakuló koordinátaváltozást tudja bemutatni,
mert a keléshez, nyugváshoz közelebbi időben az eltérés az itt láthatónak a húszszorosát is eléri. A
refrakciós változás rektaszcenzió és deklináció szerinti komponenseinek aránya az észlelés földrajzi
szélességétől függ. A piros korongok a kerek órákat jelzik.
Az ábra lényegében a delelés környéki ±4,5 óra alatt kialakuló koordinátaváltozást tudja bemutatni,
mert a keléshez, nyugváshoz közelebbi időben az eltérés az itt láthatónak a húszszorosát is eléri. A
refrakciós változás rektaszcenzió és deklináció szerinti komponenseinek aránya az észlelés földrajzi
szélességétől függ. A piros korongok a kerek órákat jelzik.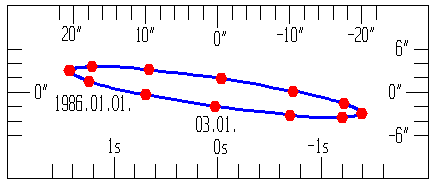
 A napi aberráció az Aldebaran esetében, Vaskútra vonatkoztatva nagyon kicsi, az évi aberráció század
része: a fél nagytengely mintegy 0,2". Ahhoz, hogy az ábra valamennyire is értékelhető legyen, az évi
aberráció ábrájához viszonyítva 16-szorosára kellett nagyítani. A piros jelek ebben az esetben két órás
időközöket jelölnek. (1986. jan. 1.)
A napi aberráció az Aldebaran esetében, Vaskútra vonatkoztatva nagyon kicsi, az évi aberráció század
része: a fél nagytengely mintegy 0,2". Ahhoz, hogy az ábra valamennyire is értékelhető legyen, az évi
aberráció ábrájához viszonyítva 16-szorosára kellett nagyítani. A piros jelek ebben az esetben két órás
időközöket jelölnek. (1986. jan. 1.)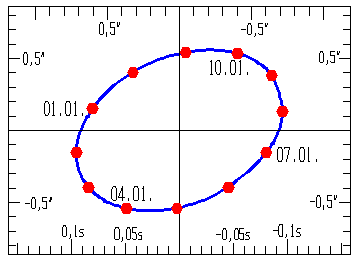
 A bal oldali ábra a Föld nevezetes pozícióit
mutatja az éves keringés során. A külső kör az éggömböt jelképezi a megfelelő rektaszcenzió
értékekkel, valamint az Aldebaran irányával.
A bal oldali ábra a Föld nevezetes pozícióit
mutatja az éves keringés során. A külső kör az éggömböt jelképezi a megfelelő rektaszcenzió
értékekkel, valamint az Aldebaran irányával.


 A nutáció számos, az ekvatoriális koordinátarendszert befolyásoló tényezőt foglal magába, de
közülük legjelentősebb Holdunk gravitációs hatása. Az ábrából látható, hogy egy hónap alatt
egy dupla spirál rajzolódik ki, amelynek "amplitúdója" néhány tized ívmásodperc.
A nutáció számos, az ekvatoriális koordinátarendszert befolyásoló tényezőt foglal magába, de
közülük legjelentősebb Holdunk gravitációs hatása. Az ábrából látható, hogy egy hónap alatt
egy dupla spirál rajzolódik ki, amelynek "amplitúdója" néhány tized ívmásodperc.